🔗 문제 링크
15591번: MooTube (Silver)
농부 존은 1번 동영상과 2번 동영상이 USADO 3을 가지고, 2번 동영상과 3번 동영상이 USADO 2를 가지고, 2번 동영상과 4번 동영상이 USADO 4를 가진다고 했다. 이것에 기반해서 1번 동영상과 3번 동영상의
www.acmicpc.net
📝 풀이 과정
문제를 보면 N까지의 영상이 존재하는데 영상끼리 가는 경로는 무조건 존재하며, 개수는 N - 1개라고 주어진다. 이것으로 주어진 그래프가 Spanning Tree(신장 트리, 최소 연결 부분 그래프)임을 알 수 있다.
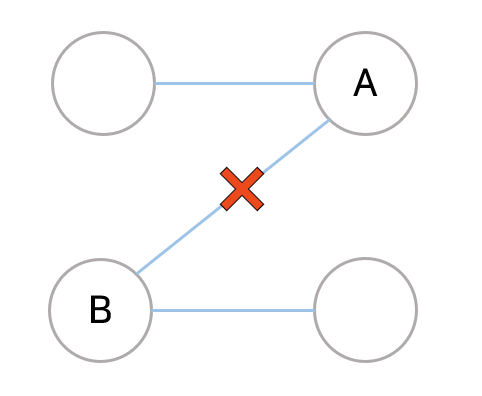
따라서, 만약 A → B로가는 연결이 끊어진다면 A → B로는 갈 수 없게 되며 A에서 출발해 B에서 연결된 다른 간선들도 도달할 수 없게 된다는 것을 의미하게 된다. 이를 활용해 BFS를 돌며 영상 사이의 거리가 K보다 작게 되면 해당 영상에서 갈 수 있는 모든 USADO의 크기가 K이하가 되기 때문에 탐색을 하지 않도록 BFS를 돌지 않도록 Queue에 추가하지 않으면 된다.
추가적으로, 간선의 개수가 노드의 개수에 비해 매우 작기 때문에 2차 배열이 아닌 ArrayList[]형태로 저장하는 것이 시간의 효율성을 증가시킨다.
⏱ 시간 복잡도
BFS를 Q번 반복하기 된다. 인접리스트 BFS의 시간복잡도는 $O(V + E)$.
따라서 시간복잡도는 $O(Q\times(V + E))$가 된다.
V와 E는 각각 최대 5000과 4999가 되지만 5000으로 생각해주었고, Q는 최대 5000이다.
$ (5000 + 5000) \times 5000 = 10^4\times5\times10^3 = 5\times10^7 < 10^8$
💻 코드
import java.util.*;
public class Main {
static final int INF = Integer.MAX_VALUE;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt(), Q = sc.nextInt();
List<int[]>[] adj = new ArrayList[N + 1];
for (int i = 1; i <= N; i++)
adj[i] = new ArrayList<>();
for (int i = 1; i < N; i++) {
int p = sc.nextInt(), q = sc.nextInt(), r = sc.nextInt();
adj[p].add(new int[]{q, r});
adj[q].add(new int[]{p, r});
}
StringBuilder sb = new StringBuilder();
for (int i = 0; i < Q; i++) {
int k = sc.nextInt(), v = sc.nextInt();
boolean[] visit = new boolean[N + 1];
visit[v] = true;
Queue<Integer> que = new LinkedList<>();
que.add(v);
int ans = 0;
while (!que.isEmpty()) {
int cur = que.poll();
for (int[] a : adj[cur]) {
if (!visit[a[0]] && a[1] >= k) {
que.add(a[0]);
visit[a[0]] = true;
ans++;
}
}
}
sb.append(ans).append('\n');
}
System.out.println(sb.toString());
}
}📊 제출 결과

'알고리즘 풀이 > 백준' 카테고리의 다른 글
| [백준] 5639번: 이진 검색 트리 - JAVA (1) | 2021.01.05 |
|---|---|
| [백준] 2638번: 치즈 - JAVA (0) | 2021.01.05 |
| [백준] 1932번: 정수 삼각형 - JAVA (0) | 2021.01.01 |
| [백준] 1786번: 찾기 - JAVA (0) | 2020.12.30 |
| [백준] 1238번: 파티 - JAVA (0) | 2020.12.21 |



